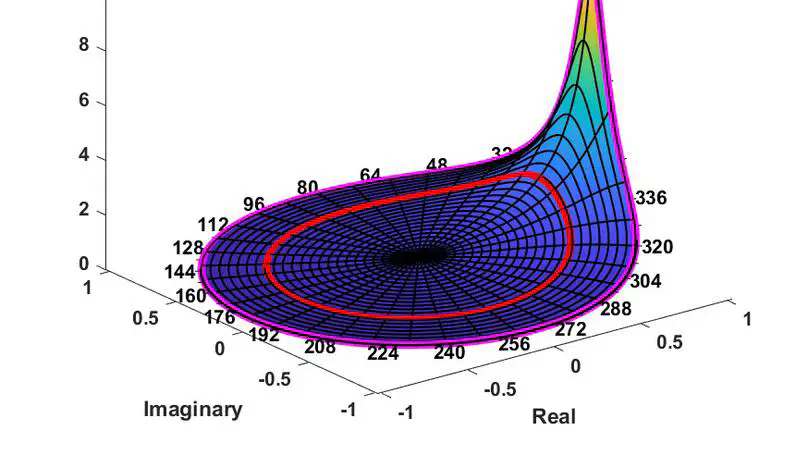
We present determinacy bounds on monetary policy in three models of inattentiveness - sticky information, imperfect common knowledge, and arbitrary finite inattentiveness. We find that these bounds are identical across these models as they all share a common vertical long run Phillips curve. The resulting bounds are more conservative than in the standard Calvo sticky price New Keynesian model. Specifically, the Taylor principle is now necessary directly - no amount of output targeting can substitute for the monetary authority’s concern for inflation. These determinacy bounds are obtained by appealing to frequency domain and forecasting/prediction innovation techniques that themselves provide novel interpretations of the Phillips curves.
An earlier version was entitled ``Sticky Information and the Taylor Principle’'.

This paper develops and implements a backward and forward error analysis of and condition numbers for the numerical stability of the solutions of linear dynamic stochastic general equilibrium (DSGE) models. Comparing seven different solution methods from the literature, I demonstrate an economically significant loss of accuracy specifically in standard, generalized Schur (or QZ) decomposition based solutions methods resulting from large backward errors in solving the associated matrix quadratic problem. This is illustrated in the monetary macro model of Smets and Wouters (2007) and two production-based asset pricing models, a simple model of external habits with a readily available symbolic solution and the model of Jermann (1998) that lacks such a symbolic solution - QZ-based numerical solutions miss the equity premium by up to several annualized percentage points for parameterizations that either match the chosen calibration targets or are nearby to the parameterization in the literature. While the numerical solution methods from the literature failed to give any indication of these potential errors, easily implementable backward-error metrics and condition numbers are shown to successfully warn of such potential inaccuracies. The analysis is then performed for a database of roughly 100 DSGE models from the literature and a large set of draws from the model of Smets and Wouters (2007). While economically relevant errors do not appear pervasive from these latter applications, accuracies that differ by several orders of magnitude persist.

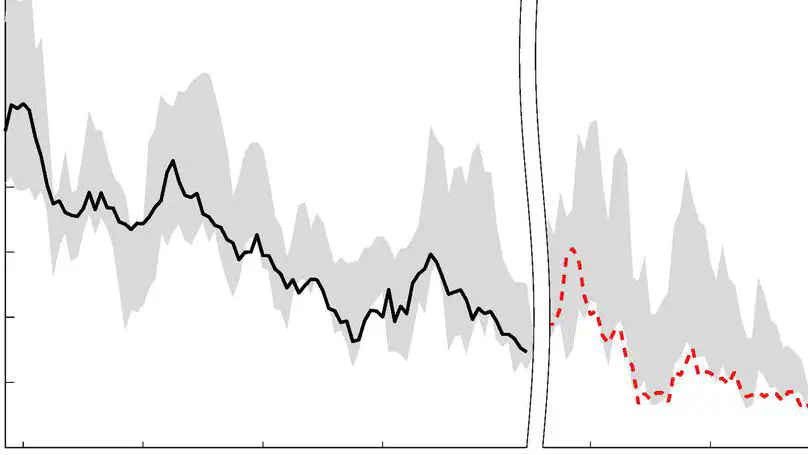
The term structure of interest rates is crucial for the transmission of monetary policy to financial markets and the macroeconomy. Disentangling the impact of monetary policy on the components of interest rates, expected short rates, and term premia is essential to understanding this channel. To accomplish this, we provide a quantitative structural model with endogenous, time‐varying term premia that are consistent with empirical findings. News about future policy, in contrast to unexpected policy shocks, has quantitatively significant effects on term premia along the entire term structure. This provides a plausible explanation for partly contradictory estimates in the empirical literature.